10025. Задача ? 1 ? 2 ? … ? n = k

Имеется формула ? 1 ? 2 ? … ? n = k. Вместо знаков ‘?’ ставятся ‘+’ или ‘-‘ так, чтобы получить верное равенство. Для заданного k найти минимальное n, для которого существует указанная формула. Например, для k = 12 ответом будет n = 7, так как - 1 + 2 + 3 + 4 + 5 + 6 - 7 = 12.

Вход. Первая строка содержит количество тестов, за которой следует пустая строка. Каждая следующая строка содержит целое число k (0 £ |k| £ 10⁹). Входные тесты разделены пустой строкой.

Выход. Для каждого теста вывести минимальное n (1 £ n), для которого существует формула, из которой можно получить k. Вывод результатов для последовательных тестов разделять пустой строкой.

Пример входа

2

12

-3646397

Пример выхода

7

2701

РЕШЕНИЕ

математика

Анализ алгоритма

Положим k = |k|, после чего k станет положительным. Ищем минимальное n, для которого 1 + 2 + … + n ³ k. Решим уравнение (1 + n) * n / 2 = k относительно n. После преобразований получим: n² + n – 2k = 0, дискриминант D = 1 + 8k, положительный корень уравнения равен

n₁ =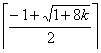

Ответом будет такое n Î {n₁, n₁ + 1, n₁ + 2}, для которого четность суммы 1 + 2 + … + n и четность k совпадают. Отдельно следует обработать случай k = 0: поскольку если 1 + 2 – 3 = 0, то ответом будет 3.

Реализация алгоритма

Читаем количество тестов tests.

scanf("%d",&tests);

while(tests--)

{

Для каждого теста вводим значение k и находим его модуль.

scanf("%d",&k); k = abs(k);

Отдельно обрабатываем случай k = 0.

if (!k) printf("3\n");

else

{

Находим положительный корень n квадратного уравнения, приведенного выше. Увеличиваем n на 1 до тех пор, пока сумма 1 + 2 + … + n = и значение k не будут иметь одинаковую четность.

n = (int)(ceil((-1 + sqrt(1 + 8.0 * k)) / 2) + 0.1);

while(((1 + n) * n / 2 - k) % 2 == 1) n++;

Выводим результат. Если тест не последний, выводим после ответа на него пустую строку.

printf("%d\n",n);

}

if (tests) printf("\n");

}